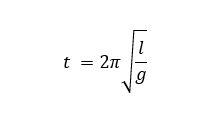"Proof" for the period of a simple pendulum using only dimensional analysis

This is not a mathematical proof for the period of a simple pendulum. For that you can find the basics in any first year physics book. This is just a thought experiment which I think illustrates the power of simple dimensional analysis.

Take the following Simple Pendulum. Its Period (t) is the time it takes for the bob to sweep through one complete cycle. Let us make the assumption that the value of t has a deterministic relation with some arrangement of measurable factors. Under this assumption we list the measurable factors.

• l = Length of the string, e.g. meters
• m = Mass of the bob, e.g. kilograms
• a = Angle to which the bob is initially lifted, e.g. radians
• g = gravitational force, length per time squared e.g. meters per second squared

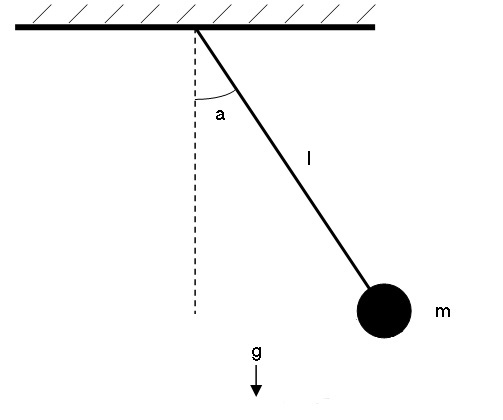
Only g has a dimensional component of time and its only other component is of distance. Only l has a dimension of distance. Thus, dimensional analysis indicates m and a cannot be related to t.

Since we know period must have the dimension of time it's a trivial task to arrange the remaining factors l and g into a formula that produces a time result. If we use seconds (s) and meters (m) as our units of time and length respectively we have:

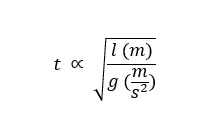
Removing unit labels and adding a constant of proportionality (k) we are left with:

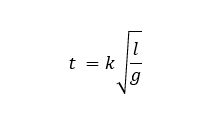
If we were to assume our new formula was valid we could experimentally measure the value of k and that value would resolve to approximately 2Pi. Thus, using only simple dimensional analysis we've generated the classical formula for the period of a Simple Pendulum.